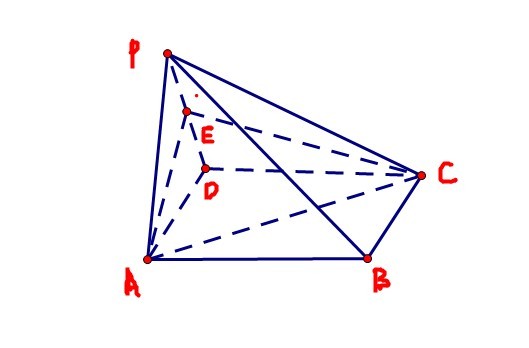
如图,四棱锥P-ABCD中,底面ABCD为正方形,PA=PD,PA垂直PD,PA垂直平面PDC, E为棱PD的中点
如图,四棱锥P-ABCD中,底面ABCD为正方形,PA=PD,PA垂直PD,PA垂直平面PDC, E为棱PD的中点
如图 四棱锥p-abcd中,底面abcd为正方形,pa=pd,pa⊥平面pdc,e为棱pd的中点
在四棱锥P-ABCD中,PD垂直于底面ABCD,底面ABCD为正方形,M为PC的中点,PD=AB,求证PA平行平面MBD
四棱锥p-ABCD中 底面ABCD为矩形,PD垂直底面,AD=PD,E F分别为CD PB 中点 求证 EF垂直平面PA
在底面为平行四边形的四棱锥P-ABCD中,AB垂直AC.PA垂直平面ABCD,且PA=AB,点E是PD的中点
在底面为平行四边形的四棱锥P-ABCD中,AB垂直AC,PA垂直平面ABCD,且PA=AB,点E是PD中点
在底面为平行四边形的四棱锥P-ABCD中,AB⊥CD,PA⊥平面ABCD且PA垂直于AB.点E是PD中点
两个平面垂直判定定理已知四棱锥P-ABCD的底面为正方形,PA垂直底面ABCD,E,F分别为AB,PD的中点,PA=2,
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=AD,点E,F分别为AB、PD的中点
如图,在四棱锥P-ABCD中,PA垂直于平面ABCD,四边形ABCD为正方形,PA=AB=4,G为PD中点,E点在AB上
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别为PA,BC的中点,PD垂直于平面ABCD,且PD=AD=根
如图,在四棱锥P一ABCD中,底面ABCD是菱形,PA垂直ABcD,M为PD的中点1求证PB